我原先是被书名吸引, 没想到还真是本讲物理史话的书。对于我们非专业的人来读,可以当历史书看,细节不用深究,还是很有意思的。
网上可以找到作者影像讲解这本书内容的视频。
上大学时开始学高数,总要开始学矩阵。但为什么要学矩阵,矩阵是如何产生的,为何要使用,它到底在整个物理或数学进程中有和意义。看这本书会让你有茅塞顿开之感。
几百年来物理学家最关注的问题是电子是粒子还是波,本书就是以此为主轴。
平滑性的假设,是微积分的基础。量子论告诉我们,“无限分割”的概念是一种数学理想,而不可能在现实中实现,一切都是不连续的,连续的美好蓝图,也许只不过是我们的一种想象。
这推翻了自牛顿以来,曾被认为是坚不可摧的经典世界。
任何时候我们观察的电子,它当然只能表现出一种属性,要么是例子要么是波。声称看到粒子一波混合叠加的人要么是老花眼,要么是纯粹在胡说八道。但是,作为电子这个整体概念来说,它却表现出一种波粒二象性来:它可以展现出粒子的一面,也可以展现出波的一面,这完全取决于我们如何去观察它。我们想看到一个粒子?那好,让它打到荧光屏上变成一个小点。看,粒子!我们想看到一个波?也行,让它通过双缝组成干涉图样。看,波!
从波粒二象性倒是让我更理解三位一体。电子是完全的粒子也是完全的波。神也是完全的父,完全的子,完全的圣灵,并不是一会儿变成父,一会儿变成子或者一会儿变成圣灵。通过我们不同角度的观察也就展现出了不同的属性,也就是基督教中讲的位格。
自此作者介绍了于奥卡姆剃刀原理,观测不到的实在世界全是子虚乌有的,至少是无意义的。
剃刀原理是说,当两种说法都能解释相同的事实时,应该相信假设少的那个。比如,地球”本来“是方的,但”观测时显现出圆形“,这和地球”本来就是圆的“说明的是同一件事。但前者引入了一个莫名其妙的不必要的假设,所以前者是胡说。
这理论在我这里是站不住的。现在我们都知道地球是圆的,是通过宇宙观测到的。中世纪以前的观测手法不同,当时也可以产生立论:地球本来是圆的,但观测时显现出方形。你也不能说这个立论是错误的。我们科学的观测手法还是太有限,不断地完善技术也是为了更靠近真相。不过作者在书中提到中世纪被活活烧死的日心说支持者布鲁诺被烧死的主要原因是神学和哲学原因。布鲁诺怀疑三位一体学说,否认玛丽亚的童贞,认为万物有灵,怀疑耶稣的生平事迹,对于地狱和犯罪的错误看法等,也包括他的一些具体行为,例如亵渎神明,侮辱教皇,试图在修道院纵火,研究和施行巫术,等等。对于宇宙和太阳行星的看法当然也包括在其中,但却远非主要部分。在科学史界有一种非常著名的看法:布鲁诺对于日心体系的支持,其根源在于赫尔墨斯主义(Hermeticisim)对其的深刻影响。赫尔墨斯主义是一种古老的宗教,带有强烈的神秘主义,泛神论和巫术色彩。这种宗教崇拜太阳,而哥白尼体系迎合了这种要求,布鲁诺的思想带着深重的宗教使命感,试图恢复这种古老巫术体系的繁荣。教会最后判了布鲁诺8项罪名,具体是哪些我们现在已经无从得知了,不过很有可能,他主要是作为一个巫师被烧死的。我觉得作者的这种说法还是比较可信的。
公理是指人类根据现实经验得出,无需自证的基本事实,《几何原本》中的五个公理包括:
1.等于同量的量彼此相等。
2.等量加等量,和相等。
3.等量减等量,差相等。
4.彼此重合的图形是全等的。
5.整体大于部分。
公设也是指无需自证的基本事实,但是相比于公理来说,公设更有深度一些,近代数学中公设等价于公理,《几何原本》中的五个公设包括:
1.过两点能作且只能作一条直线。
2.线段可以无限延长。
3.以任一点为圆心,任意长为半径可作一圆。
4.直角都相等。
5.平面内一条直线和两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线无限延长后在这一侧一定相交。
五个公设中的前四个很容易理解,基本上也不会有争议,但是大名鼎鼎的第五公设可折腾了数学家两千多年,因为第五公设看起来怎么也不像不证自明,虽然欧几里得极尽减少第五公设的语言描述,但是第五公设比前面四个公设加起来还长。
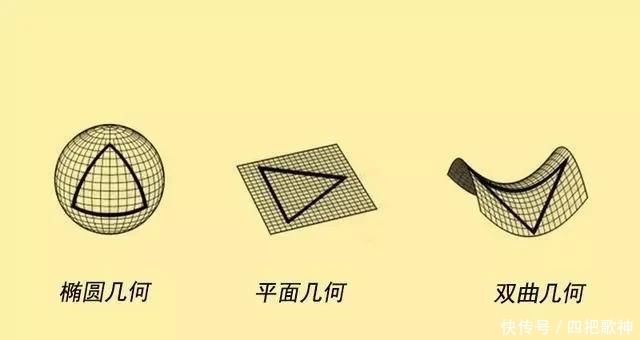
1、欧氏几何,也称作平面几何,第五公设成立,平面内三角形内角和等于180°,过直线外一点可以做一条平行线。
2、黎曼几何,也称作椭圆几何,第五公设不成立,平面内三角形内角和大于180°,过直线外一点找不到任何一条与之平行的直线。
3、罗巴切夫斯基几何,也称作双曲几何,第五公设不成立,平面内三角形内角和小于180°,过直线外一点至少可以做两条平行线。
参考资料
闲话摘录
科学史上有两个年份,便符合奇迹的称谓,而他们又是和两个天才的名字紧紧相连的。这两个年份分别是1666年和1905年,那两个天才便是牛顿和爱因斯坦。
1666年,23岁的牛顿为了躲避瘟疫,回到乡下的老家度假。在那段日子里,他一个人独立完成了几项开天辟地的工作,包括发明了微积分(流数)完成了光分解的实验分析,以及对于万有引力定理的开创性思考。在那一年,他为数学,力学和光学三大学科分别打下了基础,而其中的任何一项工作,都足以让他名列有史以来最伟大的科学家之列。很难想象,一个人的思维何以在如此短的时间内涌流出如此多的灵感,人们只能用一个拉丁文annus
mirabilis 来表示这一年,也就是奇迹年。
1905年的爱因斯坦也是这样,在专利局里蜗居的他在这一年写出了六篇论文:3月18日,是我们上面提到过的关于光电效应的文章,这成为了量子论的奠基石之一。4月30日,关于测量分子大小的论文,这为他赢得了博士学位。5月11日和后来的12月19日,两篇关于布朗运动的论文,成了分子论的里程碑。6月30日,题为《论运动物体的电动力学》的论文,这个不起眼的题目后来被加上了一个如雷贯耳的名称,叫做狭义相对论,它的意义就不用我多说了。9月27日,关于物体惯性和能量的关系,这是狭义相对论的进一步说明,并在其中提出了著名的质能方程E=mc^2。
最后书中提到德国为何在二战没有造出原子弹,是海森堡真的算错还是意识到了原子弹所引发的道德问题故意的消极怠工?
记得我上高中时就看过话剧Die Physiker,科技发展的迅猛超过我们的想象,当我们打开潘多拉的魔盒,我们还能很好的控制它吗?想来也是现今一直探讨的问题。
量子论历史大事记
1900年,Max Planck 提出量子的概念。
1924年,Louisde Brogie 提出光的粒子行为与粒子的波动性为应该是对应存在的。
1924年,S.N. Bose 提出光遵循一种建立在粒子不可区分的性质(及全同性)上的一种新的统计理论。
1925年,Wemer Karl Heisenberg、Max Born、pascual Jordan 提出了量子力学的第一个版本。
1925年,Wolfgang Ernst Pauli提出了量子力学的第二种形式,波动力学。
1926年,Erwin Schrodinger 提出了波动方程。
1927年,Niels Bohr提出互补原理,试图解释量子理论中一些明显的矛盾,特别是波粒二象性。
1927年,Heisenberg 阐明测不准原理。
1928年,Paul Dirac 提出了相对论性的波动方程来描述电子,解释了电子的自旋并且预测了反物质。



Kommentar schreiben